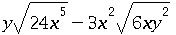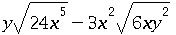Postby Doubleshadow » Fri Apr 27, 2007 1:49 pm
It's probably way too late, but here it is:
When the number under the radical doesn't have an easy square root, break it down into factors that do. So,
SQR(24) = SQR(4*6)
because we know the square root of 4 is 2, we can move it to the outside and get
2SQR(6)
The same is true for variables with exponents.
SQR(x^5) = SQR(x^4 *x)
Since the square root of x^4 is x^2, it can be moved out side the radical and we get
(x^2)SQR(x)
In the case of y^2, its just the square root of y^2 which is y. Remember, the square root of anything squared is itself.
After that, group common factors so that
(x^2)*y*SQR(6x)*(2-3)
Since 2-3=-1, the answer is
-(x^2)*y*SQR(6x)
[color="Red"]As a man thinks in his heart, so is he. - Proverbs 23:7[/color]
The Sundries
Robin: "If we close our eyes, we can't see anything."
Batman: "A sound observation, Robin."